Random Graph Partitioning With Perfect Difference Sets Part 1/2
In which we talk about vertex separators.
Hi, Yucheng here. Thanks for reading! This is my first post, and please give feedback on what you want to hear more about! I plan to write more on technical topics on systems, databases and ML, as well as the occasional controversial opinion. More about me: I did my PhD on a graph compute abstraction for Machine Learning called GraphLab which recently received the VLDB 2023 Test Of Time Award (a reflections blog post coming soon). I was Chief Architect at a startup called GraphLab/Dato/Turi (same company) which was acquired by Apple in 2016. Now I am the CEO/Cofounder at Xethub working on data/model versioning for ML teams.
This is the 1st part of a 2 part post describing a bit of unpublished random graph partitioning work from 2012 as part of PowerGraph. It was implemented and open sourced but with very little description. I have always wanted to share it, but didn’t want to put in the experimental work to make it a conference publication, so I am sharing it here. I am probably not going to run more experiments and just use old graphs I am able to dig up from my email archives.
Technical TLDR; using Perfect Difference Sets (PDS) to partition the edges of graph can half the communication volume compared to random 2D partitoning. This is a one-pass coordination-free algorithm with some limitations (#machines = p^2 + p + 1).
This first post will set up the basic context around the problem, and the next post will describe the PDS solution.
At that time we were working on distributed graph algorithms (PageRank was a popular benchmark then). The first challenge of distributed graphs is …. distributing the graph: how to partition the graph across machines.tpa
Vertex Partition (Edge Separators)
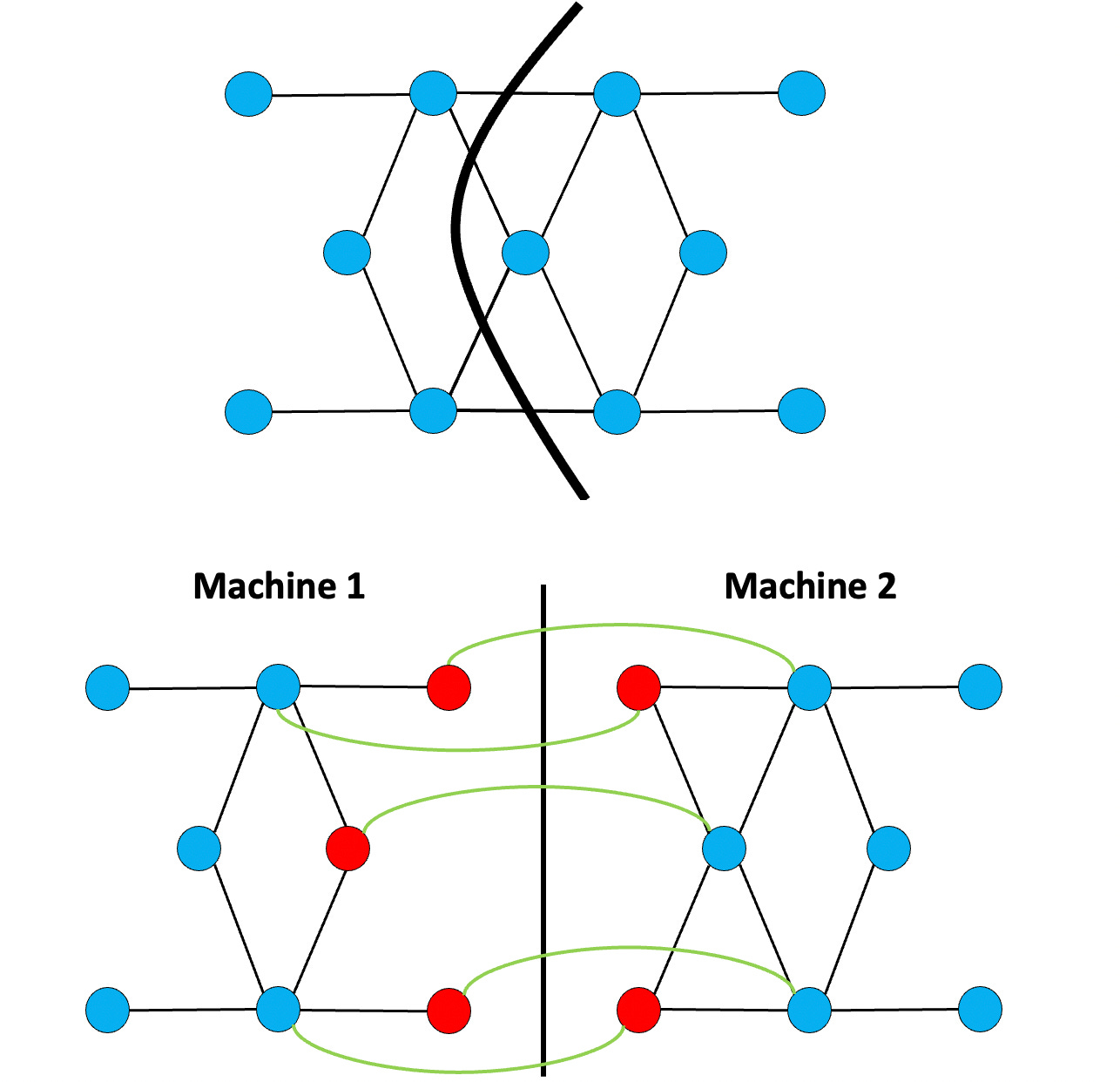
The natural way to think about graph partitioning is to place vertices on machines and let edges span machines.
This is nice and intuitive as we normally think about vertices as “entities” (ex: webpages) and so the idea of partitioning the graph using vertices is pretty easy. The red nodes indicate “ghost vertices”, which is a bit of metadata that indicate that “this vertex is on this other machine”. The memory consumption on each machine is therefore the number of vertices it is assigned, plus the set of ghost vertices.
The amount of communication required for each round of computation is proportionate to the number of edges cut. The balanced cut problem is in general NP-Hard, but there are pretty good heuristic solvers like as Metis.
In the PowerGraph paper, we showed that this method of partitioning does not work well for natural real world power-law graphs (like social networks).
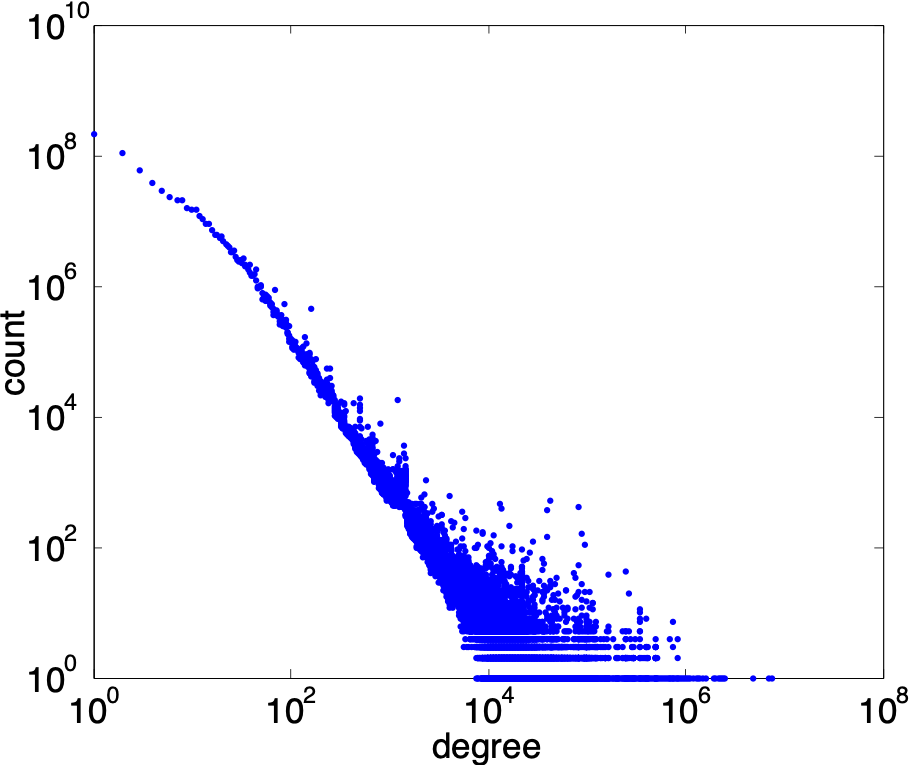
Above is the degree distribution of the Yahoo! Altavista Web Graph 2002 (1.4B vertices 6.7B edges). These graphs do not partition well. Notably the top 100 vertices cover 1% of the edges, and the top 1% of the vertices cover 53% of the edges. These graphs do not partition well and are inherently extremely inbalanced.
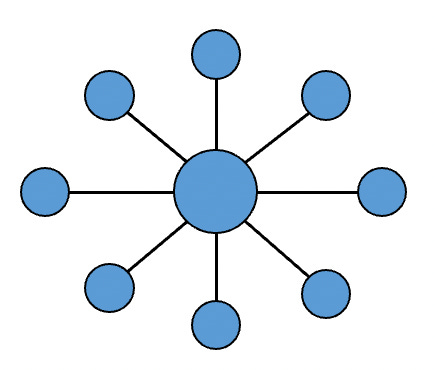
To take as a simple example, a single star graph:
It is easy to see that there is no effective partitioning of this graph. Whichever machine is assigned the central node must “ghost” the entire graph so does all the work.
There has to be a better way.
Edge Partition (Vertex Separators)
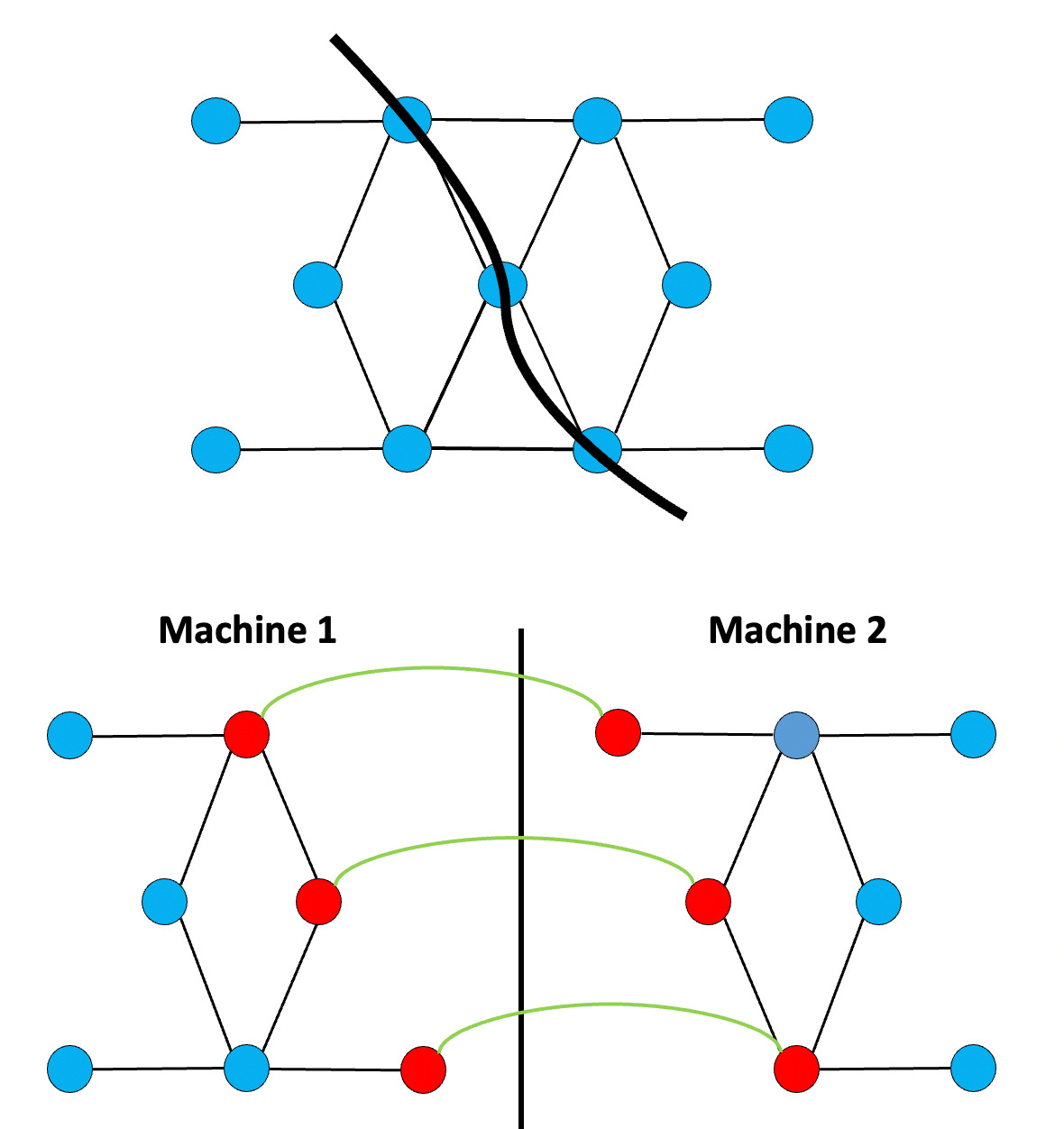
In PowerGraph, we showed an alternative less intuitive solution: that is to place edges on machines, and let vertices span machines.
This is a little bit less intuitive. But it works if you think how in many algorithms, computation is represented by the edges, and state is represented by the vertex. For instance in PageRank: the compute work is in performing a sum over all the edges, and the state is the current PageRank value on each vertex. Then this representation balances the “work”, and replicates the “state” which is pretty much exactly what you want. While not all algorithms map onto this layout efficiently, a remarkably large number do.
What else is remarkable is if we compare randomized cuts. If given a very large graph, the work needed to compute a good “partition” may not be worth it. In which case the simple thing to do will be do a random partition. That is if I am partitioning vertices as in the previous section: I just randomly place vertices onto machines. And if I am partitioning edges as in this section, I just randomly place edges onto machines.
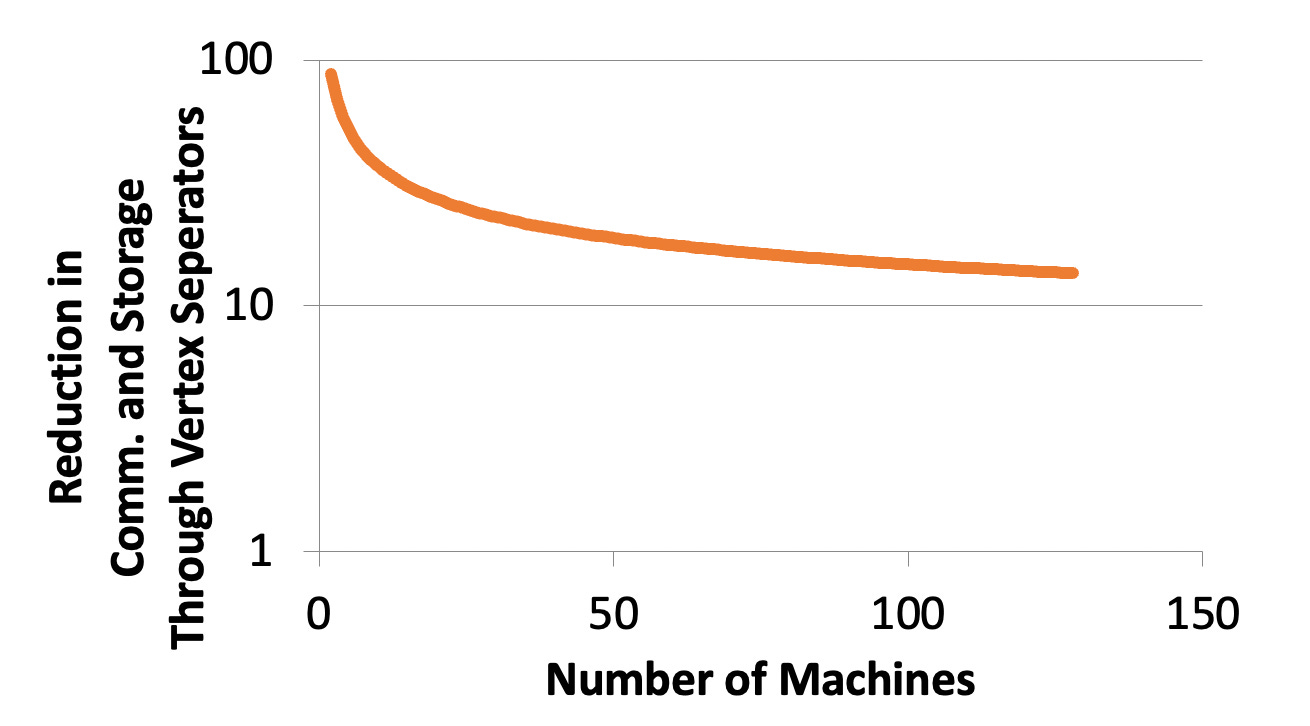
We can demonstrate mathematically that the partitioning edges gives at least an order of magnitude reduction in communication compared to partitioning vertices.
Further Improvements
Now, there are of course a lot of optimizations one can make beyond a random partition, even in a coordination-free way. We explore these in the next part and how we can use Perfect Difference Sets to make a difference.
Another Hammer In a Toolbox
A question one may ask is, why even bother? I am not working on graph algorithms, much less distributed ones. I see this as simply another tool in an architects tool chest of abstractions. One of the key challenges facing any systems architect is “how to represent data/state and where to store it”. There are innumerable perspectives one can take. After all, this is one of the fundamental problems of Computer Science: data structure selection and design.
A surprisingly large number of problems can be interpreted as a graph, and the different ways to partition it introduces a different perspective for looking at a problem.
For instance, consider a classical system design interview question: design the twitter feed. One way to interpret the problem is that this a bipartite graph between users and feeds. The edge partition model above then provides an entirely different view of how the celebrity problem might be addressed. This is left as an exercise for the reader.